ОСНОВЫ ОБЩЕЙ ФИЗИКИ
КОЛЕБАНИЯ В КРИСТАЛЛАХ
Кристалл представляет собой
совокупность атомов, связанных упругими
силами. В зависимости от расположения
атомов кристаллическая решетка может быть
простой, гранецентрированной,
объемноцентрированной и т.д. При малых
амплитудах смещения атомов из их положения
равновесия справедливо гармоническое
приближение описания колебаний. Под
действием теплового возбуждения атомы в
кристалле находятся в непрерывном
движении.
Рассмотрим колебания атомов в одномерном кристалле. Представим такой кристалл в виде цепочки шариков с массами m1 и m2, соединенных пружинами с жесткостью c. Сила, действующая на каждый шарик, зависит от относительного смещения двух других шариков, лежащих справа и слева от рассматриваемого. Поэтому, смещение каждого шарика un и um (см. рисунок) задается следующей системой уравнений:
m1(d2un/dt2)
= -c(2un - um-1
- um)
m2(d2um/dt2)
= -c(2um - un
- un+1)
Эти уравнения описывают колебательное движение атомов в одномерном кристалле:
un = A1exp{
i(kan-wt)
}
um= A2exp{
i(kam-wt)
}
где a/2 - расстояние между ближайшими атомами, k=2p/l - волновое число, l - длина волны в кристалле. Уравнения, приведенные выше, имеют два решения относительно w:
w12 =
(w02/2) [ 1 - (1-g2sin2(ak/2))1/2
]
w22= (w02/2)
[ 1 + (1-g2sin2(ak/2))1/2
]
где g2 = 4m1m2/(m1+m2)2; w02 = 2c (m1+m2)/m1m2. Эти уравнения определяют две ветви дисперсионной кривой (так называемая акустическая ветвь и оптическая ветвь).
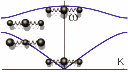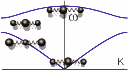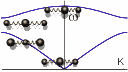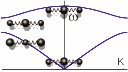На
рисунке слева показаны акустическая и оптическая ветви дисперсионной кривой для
колебаний в одномерном кристалле (т.е. зависимость частоты волны
ω
от волнового числа
k=2π/λ
). В
предельном случае длинных волн в
акустической ветви колебаний w1
атомы движутся синхронно и отклонения в
каждый момент времени одинаковы (самая нижняя анимация на рисунке слева). В
оптической ветви атомы колеблются в
противоположных фазах, так что их центр
масс неподвижен: m1un
+ m2um+ ... = 0 (самая верхняя
анимация на рисунке слева). При этом, если ячейка сложного кристалла состоит из
разноименных ионов, то колебания в оптической ветви связаны с изменением
электрического дипольного момента ячейки и могут проявляться при поглощении и
испускании инфракрасного излучения. Этим и объясняется название этой ветви
дисперсионной кривой. Для предельно коротких волн в акустической ветви
неподвижны более легкие атомы, а колеблются более тяжёлые. В оптической ветви
колебаний - наоборот, неподвижны более тяжёлые атомы, а колеблются более лёгкие
(две средние анимации на рисунке слева).
Внутренняя энергия кристалла заключена в виде потенциальной энергии деформации виртуальных пружин, соединяющих атомы, и в виде кинетической энергии вибрации атомов. Эти два вида энергии постоянно переходят из одной формы в другую. При этом температура кристалла пропорциональна средней кинетической энергии атомов. Имеются также некоторые ограничения на анализ тепловых колебаний в кристалле, проведенных с точки зрения классической механики. Так как мы имеем дело с объектами сопоставимыми по размерам с отдельным атомом кристалла, нельзя пренебречь квантовомеханическими эффектами.
Рассмотрев приведенные выше формулы для колебаний атомов в одномерном кристалле un и um, мы видим, что эти формулы идентичны выражению для линейной волны с угловой частотой w и волновым числом k. Подобно электромагнитной волне, колебания атомов в кристалле проявляют корпускулярные свойства, и волнам в кристаллах ставится в соответствие виртуальная частица ФОНОН - квант упругих колебаний, обладающая энергией и импульсом. С этой точки зрения внутренняя энергия кристалла может быть рассмотрена как суммарная энергия движущихся фононов.
